[로고스토리] 장(Field)과 선속(Flux)

장(Field) 이란, 기본적으로 위치벡터에 대응되는 특정한 물리량의 함수를 의미합니다.
대표적으로, 위치벡터에 따라 각 위치 벡터에 따른 힘의 크기와 방향이 대응되는 중력장과 전기장이  그 예시입니다. 

물리량이 스칼라와 벡터라는 두가지의 방법으로 기술 되듯이, 물리량의 함수인 '장' 역시도 스칼라장과 벡터장이 나뉘어 져 있습니다. 위치벡터에 따라 대응되는 물리량이 스칼라이면 스칼라장, 벡터이면 벡터장이라고 할 수 있습니다.

장의 수학적 표기법은 그 정의에서도 볼수 있다시피 일정한 공간의 함수로 나타낼 수 있는데,
스칼라 장은 V(x,y,z) 로 나타내어지고, 벡터장은 F<P(x,y,z), Q(x,y,z), R(x,y,z)> (공간에 대한 함수를 성분으로 가지는 벡터 함수의 형태로 표기됨) 과 같은 형태로 나타내어 지게 됩니다.

이렇듯 장이라는 개념은 해당 장에 놓은 물체의 운동을 기술하거나 혹은 장 그자체의 변화에 의한 물리적 현상들을
관찰하기 위하여 중요한 개념이라고 할 수 있습니다.

그렇다면 장은 수학적으로 어떻게 분석할 수 있을까요?

'델 연산자(Del Operator)' 를 이용한 연산 그레디언트 (gradient), 발산 (divergence), 회전 (curl), 라플라시안 (Laplacian)
위의 연산자들을 이용하여 장을 수학적으로 분석할 수 있습니다.

우선 델 연산자는 다음과 같은 정의를 가지고 있는 연산자로서

(직교좌표계에서, e_i 의 경우 i 번째의 좌표에서 1이고, 나머지 좌표에서는 0이다.)

또한 이 델연산자를 이용한 연산자들에 대해서
각각 다음과 같은 표현이 그레디언트, 발산, 회전, 라플라시안의 정의입니다.

 

1. 그레디언트 (gradient)

그레디언트는 다음과 같이 정의 되며, 스칼라장의 기울기를 나타낼 떄 사용된다. (스칼라장의 변화량이 가장 큰 방향을 가리키는 벡터)

2. 발산 (divergence)

3차원 직교좌표계에서의 정의

또는

발산은 벡터장에서 정의되며, 기저벡터의 성분 함수의 편도함수들의 합으로 정의 된다. 또한 그 의미는 국소적인 부분에서 유출되거나 유입되는 선속 (후에 다룸) 의 양을 의미한다.

 

적분을 이용한 정성적 의미에서의 표기

 

3. 회전 (curl)

회전은 3차원 벡터장에서 정의되며, 벡터장의 회전을 정량적으로 나타낸다.

 

4. 라플라시안 (Laplacian)

라플라시안은 스칼라장에서 정의 되며, 스칼라장의 기울기 벡터의 발산으로써 정의 된다.

 

벡터장의 라플라시안.

 

 

 

이러한 수학적 기술들을 이용하여 장에 대해서 분석할 수 있습니다.
물리학에서 이렇게 수학적으로 장에 대한 분석은 다양한 방정식에서 등장하게 되는데요.

가장 유명한 방정식이 맥스웰 방정식 (Maxwell's Equation) 과 나비에 - 스토크스 방정식( Navier-Stokes Equations ) 일 것입니다.

 

맥스웰 방정식, 이는 미분형으로 나타낸 것이다.

 

나비에 스토크스 방정식

 

이렇듯 장을 분석하는 것은 실재의 물리적 상황을 해석하는 것에 큰 도움이 되고, 또한 꼭 필요한 기술입니다.

그렇다면 이제 장을 분석하기 위한 또 다른 개념에 대해서 설명드리겠습니다. 바로 '선속 (Flux)'  입니다.

 

 

선속 (Flux)

선속이란, 면적을 지나는 벡터장의 양을 나타낸 수치입니다. 수학적으로 선속을 정의 내릴때, 다음과 같이 면적분을 이용하여 나타낼 수 있습니다.

수식적으로 볼때, 상당히 난해해보이는 설명이지만, 이것을 그림으로 나타내어 이해해보면 한 층 쉽게 다가오실 겁니다.

 

그림을 보면, dS 는 해당 면적의 미분소를 나타내고, n 벡터는 해당 면적의 면적벡터입니다. 또한 벡터장 F 가 지나갈때,

해당 벡터장을 면적벡터 n 에 대해 내적합니다. 그렇다면, 면적벡터 n 과 같은 방향을 가진 벡터장 F 의 세기가 남게 될것입니다. 

이를 이용하여 선속을 다시 이해해보면, 미소 면적 dA 를 지나는 모든 벡터장 F 를 전체 폐곡면으로 적분한 양.
즉, 단위 면적당 벡터장이 지나간 양이라고 생각해 볼 수 있습니다.

수학적인 정의로 생각하여 볼때, 선속의 정의는 앞서 소개하였던 '발산' 과 꽤나 유사한 점이 많다고 생각이 들 수 있습니다. 
실제로도 그렇습니다. 

발산의 정의는 '국소적인 부분에서의 벡터장의 유입 (또는 유출량)' 으로 이를 3차원 공간에서는 국소적인 부피,
혹은 부피의 표면에서 빠져나가는 양이라고 할 수 있습니다, 이는 바꾸어 말하면, 
발산은 미소 부피에서의 선속으로 생각 해볼 수 있습니다. 선속을 부피에 관한 식으로 규격화하면 다음과 같이
나타낼 수 있습니다.

이를 발산 정리라고 함

 

그렇다면, 이 선속은 어떠한 의미를 가지고 있을까요? 
앞서 선속은 '단위 면적당 벡터장이 지나간 양' 이라고 하였습니다. 
즉, 이는 단위 면적당 벡터장, 즉 벡터장의 세기와 같다는 것입니다.

즉, 선속은 벡터장의 세기를 나타내는 물리량이 될 수 있습니다.
물리적으로 의미를 가지는 선속이 사용되는 법칙의 예시로 그 의미를 알아보도록 하겠습니다.

가우스 법칙

임의의 폐곡면 내부에 전하를 띈 입자가 있습니다. 이때 전기장을 어떻게 구할 수 있을까요?
가우스 법칙은 바로 이런 문제를 해결하기 위하여 필요한 법칙입니다.
또한 가우스 법칙은 선속의 정의에서부터 유도 되었습니다.


전기 선속의 정의에서

임의의 가우스 곡면 S를 폐곡면으로 설정 한 뒤, 해당 선속의 정의를 전기장과 면적 벡터의 내적으로 형태를 바꿔 줍니다.

 

여기서 적분 기호 내부의 항만 고려해 줍니다. 또한 면적 벡터의 정의를 이용하여 다음과 같이 나타낼 수 있을 것입니다.

여기서 임의의 가우스 곡면의 미소면적 da 는 구면의 입체각을 이용하여 다음과 같이 바꿀 수 있습니다.

또한 입체각의 정의상, 다음과 같이 나타낼 수 있습니다.

이를 대입하여 양변을 적분하면, 

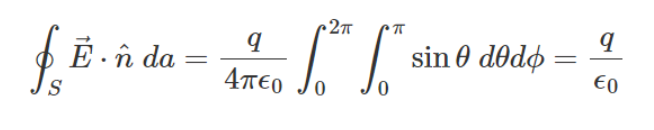
따라서 전기 선속은 그 내부 전하량에 비례하고 진공일때의 유전율에 반비례 한다는 결과에 대해서 알 수 있습니다.

그렇다면 전기장이 아닌 다른 장에서도 이러한 규칙이 적용될 수 있을까요?
당연합니다. 이를 중력장에서 유도하면, 중력 선속의 크기, 즉, 중력장이 무엇에 비례하는지에 대해서 알아낼 수있 고,
또한 중력장에 대해서 수학적으로 정리 할 수 있습니다.

(중력장은 뉴턴의 만유인력의 법칙으로 부터, 다음과 같이 유도 된다.) 

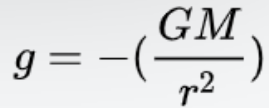
또한 실제로는 중력원 (source of gravity) 으로 부터의 위치 벡터 이므로 , 중력장은 다음과 같이 표기 할 수 있습니다.
(또한 중력원과 물체 사이의 벡터를 나타내기 위하여 원점으로 부터 두 벡터를 뺀 상태로 정의한다.)

이를 선속에 정의에 맞게 식을 짜 주면, 다음과 같다.

또한 중력장의 식에 맞게 변형하여 주면, 

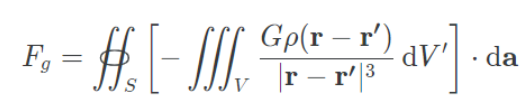
여기서 부피인 V에 대한 적분은 페곡면 S에 대한 적분에  대해서 독립이므로 다음과 같이 적분식을 수정할 수 있다.

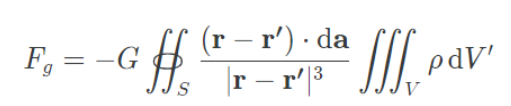
이를 가우스 법칙에서 유도한 내용으로  유도해 준다면, (밀도를 부피에 대해서 적분한 항은 중력원의 전체 질량과 같다.)

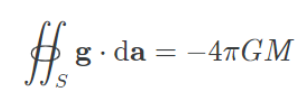
다음과 같이 유도해낼 수 있다. 

즉 중력선속은 중력원의 비례한다는 것을 알아낼 수 있었다.

또한 앞서 소개한 발산정리를 이용하면, 위의 식을 다음과 같은 형태로 고칠 수 있다.

위의 식에서,

또한 위의 부피는 임의의 부피이므로 임의의 부피에 대해서 중력장의 발산은 다음과 같이 정의됨을 알 수 있다.

또한 이를 중력장과 중력 퍼텐셜에 관한 관계를 이용하여 식을 한 번 더 변환 할 수 있는데, 
중력은 기본적으로 보존력이고, 따라서 퍼텐셜을 정의할 수 있다. (보존력과 퍼텔셜에 대해선 추후에 다뤄볼 예정)

또한 퍼텐셜과 장의 관계는 다음과 같다. 

(장은 퍼텐셜의 기울기에 음수를 취한것과 같다.)

따라서 위의 중력장에 관한 식을 퍼텐셜에 관한 식으로 수정에 주면 다음과 같은 형태의 식이 유도될 것이다.

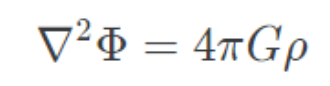
해당 방정식은 푸아송 방정식(Poisson's Equation) 으로 우리는 일반적인 선속에 대해, 해당 장이 보존력의 조건을 만족하여 보존장이 존재한다면, 이 편미분방정식을 통해 퍼텐셜에 대한 함수를 유도 해낼 수 있다.
(전기장도 보존장 이므로 푸아송 방정식 형태로 고칠 수 있다. 그러나 자기장은 보존장이 아니다)

by. 나서준