평소 스피커를 이용해 노래를 들으면서 저음이 조금 더 강조되었으면 하는 생각을 하곤 했다. 스피커에서 저음을 강화하는 방법은 여러 가지가 있다.
1. 오디오 사운드 조절
오디오 사운드를 조절하는 것은 가장 쉽게 할 수 있는 방법이다. 설정에서 저음의 레벨을 올리는 것이다. 하지만 이 방법은 앰프 자체의 출력이 높지 않으면 소용이 없다.
2. 백로드혼 구조
백로드혼 구조는 스피커의 유닛 뒤쪽에 길고 큰 소리의 통로를 만드는 것이다. 백로드혼 구조는 하나의 유닛을 사용하는 스피커에서 사용할 수 있는 방법이다. 하지만 이 방법은 만들기 매우 복잡하고 정밀하게 만들지 않는다면 들었을 때 큰 변화를 느끼기 힘들다.

3. 유닛 자체의 네트워크 보강
스피커의 유닛은 소리의 신호를 진동시키는 부분을 말한다. 재생할 수 있는 주파수 대역에 따라 트위터, 미들레인지, 우퍼로 나뉜다. 저음을 담당하는 우퍼의 네트워크를 조정해 저음을 강조할 수 있다. 이 방법은 스피커의 주파수 대역을 내가 원하는 대로 구성할 수 있다는 장점이 있지만 네트워크를 직접 만들어야 해 번거롭다.
위 세 가지 방법 중, 나는 유닛 자체의 네트워크를 보강하는 방법을 택했다. 따라서 세 가지 종류의 유닛을 사용하여 저음을 강화할 수 있는 스피커를 제작해볼 것이다.
트위터는 고음, 우퍼는 저음, 그 사이음을 미드레인지가 담당한다. 앰프에서 나온 소리를 크로스오버 네트워크를 사용해 각 유닛에 맞는 주파수 대역을 걸러주어야 한다.
각 유닛에 맞는 주파수 대역을 만들 땐 low-pass filter, high-pass filter, band-pass filter를 사용한다.
high-pass filter와 low-pass filter가 작동하는 원리를 알아보기 위해선 먼저 라플라스 변환에 대해 알아야 한다.
라플라스 변환에 대해 모른다면 아래 글을 보자.
라플라스 변환은 미분방정식을 다른 공간으로 변환시켜 단순하게 만들 때 사용하는 적분 변환의 한 종류이다. 적분 변환은 적분을 이용해 어떤 함수를 다른 함수 위로 투영시키는 방법이다.
적분변환의 수학적 정의는 다음과 같다.
$$ T[f(u)]=\int_{u_1}^{u_2}k(u, v)f(u)du = F(v)$$
$k(u, v)$는 u와 v의 함수이고 커널 함수라고 부른다.
함수 f(u)에 커널함수 k(u, v)를 곱한 후 정적분하면 v에 대한 함수가 된다.
이해를 돕기위한 간단한 예시를 들어보면
$$\int_{1}^{2}{\color{blue}xe^{-x}}dx=\frac{2e-3}{e^2}\approx 0.32975$$
$$\int_{1}^{2}{\color{blue} 2xe^{-2x}}dx=\frac{3e^2-5}{2e^4}\approx0.15721 $$
위 두 적분 값이 약 $\frac{1}{2}$배 차이나는 것을 볼 수 있다. 만약 x앞의 계수를 s라고 한다면 정적분 값을 s에 대한 함수로 나타낼 수 있을 것이다.
이처럼 x에 대한 함수를 x가 아닌 다른 변수에 대한 함수로 적분을 통해 바꾸는 것이 적분변환이다.
라플라스 변환은 커널함수가 $e^{-st}$인 적분 변환이다. $s=\sigma -j\omega $
수학적 정의는 다음과 같다.
$$L[f(t)]=F(s)=\int_{0}^{\infty}f(t)e^{-st}dt$$
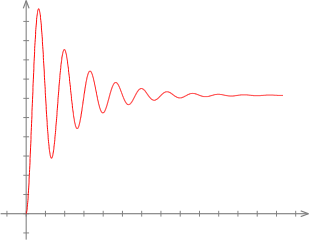
물리학적 의미를 살펴보자면 $e^{-st}$는 $e^{j\omega t}$에다가 $e^{\sigma t}를 곱한 값이다.
즉, 감쇠 진동을 분석하지 못하는 푸리에 변환의 한계를 극복하기 위해 만들어진 것이다.
라플라스 변환에 대해 알았으니 high-pass filter와 low-pass filter에 대해 알아보자.
1. High-pass filter

High-pass filter는 높은 주파수 대역은 통과시키고 낮은 주파수 대역은 차단하는 회로이다. 스피커에선 트위터와 연결한다.
캐페시터의 임피던스는 다음과 같은 공식으로 구한다.
$$X_c=\frac{1}{2\pi fc}$$
임피던스는 교류 전류의 흐름을 방해하는 것이다. 직류 회로에서의 저항과 비슷하다.
고주파성분은 진동수가 커 캐페시터의 임피던스 값이 작아져 쉽게 통과할 수 있다. 통과한 고주파성분은 연결한 스피커 유닛으로 출력된다.
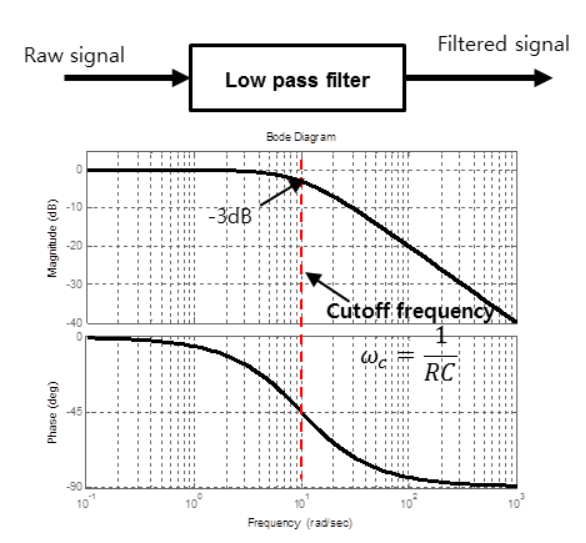
2. Low-pass filter

low-pass filter는 높은 주파수는 차단하고 낮은 주파수는 통과시키는 회로이다. 스피커에선 우퍼와 연결한다. 위와 같은 이유로 캐페시터가 차단한 낮은 대역의 주파수가 스피커 유닛에 출력된다.
이제 원리를 알았으니 캐페시터와 저항의 값을 조정해 각 유닛이 원하는 대역의 소리를 내도록 해야한다.
이는 주파수 응답을 이용해 구한다. 주파수 응답은 입력 전압 대비 출력 전압을 말한다.
다음과 같은 방법으로 각 필터의 주파수 응답을 구할 수 있다.
1. low-pass filter
$$V_c=\frac{Q}{C}=\frac{1}{C}\int i_cdt$$
$$i_c+i_R=0$$
$$c\frac{\mathrm{d} V}{\mathrm{d} t}+\frac{V}{R}=0$$
위 미분방정식을 풀면 전압을 구할 수 있다.
$$V=V_0e^{-\frac{t}{RC}$$
주파수 응답을 구할 때 필요한 입력 전압과 출력 전압을 구하는 과정은 다음과 같다.
$$V_{out}(t)=\frac{1}{C}\int_{0}^{t}I(t)dt$$
이 식을 라플라스 변환을 이용해 s에 관한 식으로 간단하게 표현할 수 있다.
$$V_{out}(s)=\frac{1}{Cs}I(s)$$
입력전압도 마찬가지로 구해준다.
$$V_{in}(t)=I(t)R+\frac{1}{C}\int_{0}^{t}I(t)dt$$
$$ V_{out}(s)=I(s)R+\frac{1}{Cs}I(s)$$
주파수 응답은 $H=\frac{V_{out}}{V_{in}}$ 이므로 low pass filter의 주파수 응답은 다음과 같다.
$$\frac{1}{1+RCs}$$
2. High-pass filter
low-pass filter와 마찬가지로 출력 전압과 입력 전압을 구하면 다음과 같은 주파수 응답을 볼 수 있다.
$$V_{out}(t)=RI(t)$$
라플라스 변환하면
$$V_{out}(s)=RI(s)$$
$V_{in}$은 low pass filter와 같으므로 주파수 응답은 다음과 같다.
$$\frac{RCs}{1+RCs}$$

이러한 내용을 이용해 각 유닛과 필터를 연결해 풍성한 소리를 내는 3-way 스피커를 제작할 수 있다.
XSim 이라는 스피커 네트워크 설계 프로그램을 이용해 주파수 응답을 알아보았다.



위에서 설계한 내용을 바탕으로 스피커 네크워크를 제작하였고 스피커를 완성하였다.


by. 1118 홍유진
(같이 스피커를 제작한 팀 : 김민준, 양민준, 소호연, 김지은)
'로고스토리' 카테고리의 다른 글
| [로고스토리] 게이지 변환(Gauge Transformation) (0) | 2024.02.20 |
|---|---|
| [로고스토리] 장(Field)과 선속(Flux) (1) | 2024.01.28 |
| [로고스토리] 확산 문제를 위한 유한체적법 (2) | 2024.01.01 |
| [로고스토리] 표준모형과 입자검출방식의 이해 (1) | 2023.12.26 |
| [로고스토리] 라그랑주 역학과 미분 기하학의 상관관계 (2) | 2023.12.26 |



