우리가 뉴턴 역학은 일반적으로 세상을 힘이라는 안경을 통해 분석해 낸다.
그런데 여기 또다른 관점으로 세상을 바라보는 학문이 있다. 그렇다 바로 라그랑주 역학이다. 라그랑주 역학은 물체가 움직일 때는 ‘액션’이라는 요소가 최소로 작용하는 방향으로 움직인다.
주장하는데, 대표적인 해석의 차이를 보자면, “어머 사과가 떨어지고 있네!” 라는 생각을 가질 때, 뉴턴 학파들은 “하하 중력은 오직 수직 방향으로 작용하기에 당연히도 이런 운동을 해야지!” 라고 주장하는 반면, 라그랑주 역학은 “하하 오직 일직선으로 아래로 내려가는게, 거리 즉 액션이 최소화 되는 경로이기에 이렇게 움직이는 게 당연하지”라는 주장을 펼칠 것이라는 것이다.
그런데 수학에도 이런 라그랑주 역학과 비슷한 논리가 하나 있는데, 바로 미분기하학에서 최소 에너지 정리다.
라그랑주에서는 ‘액션’이 최소화 되는 현상으로 운동이 일어난다고 하지만, 미분기하학에서는 ‘에너지’가 최소화된다는 원리로 물체가 움직인다는 것이다.
솔직히 이 둘의 차이점은 쉬림프버거와 새우버거의 차이 정도로 매우 유사하다는 것을 느낄 수 있다.(둘 다 최소화 되잖아) 근데 우리가 아는 라그랑주 역학의 기본 원리는 오일러 라그랑주 방정식으로부터 비롯된다는 것을 알 수 있다.
그렇다면 미분 기하학도 이 방정식을 사용할까? 아니 그렇지 않다.
미분기하학에서는 크리스토펠 심볼을 이용해 측지선 방정식을 계산해내서 상황을 해석한다. 크리스토펠 심볼이 뭐고, 측지선 방정식이 뭔지 매우 궁금할거다.
당연히도 2차원 평면에서 가장 짧은 경로는 직선일 것이다. 그렇다면 다차원 곡면에서 점과 점 사이 가장 짧은 경로도 무작정 직선을 그으면 해결될까? 답은 당연히 ‘아니오’ 이고 이 문제의 정답을 바로 측지선이라고 한다.
다차원 곡면상에서의 가장 짧은 경로 이걸 이용해서 뭘 할 수 있냐고? 우리가 아는 운동에너지와 위치에너지같은 물리량을 이 다차원의 곡률로 변환한다고 한다고 한다.
이게 뭔 소리냐고? 그니까 원래 그냥 구불거리는 평면 하나가 있다고 하자. 이게 그냥 일반적인 세계야 머릿속에 그렸지, 니가 근데 그 세계에 운동에너지와 위치에너지라는 설정을 그 세계에 막 추가 시켰어, 그러면 니가 상상한 구불거리는 평면은 이전과는 다른 모양을 띌거야, 보다 구불거리거나, 조금은 평평해지거나 그래졌겠지.
근데 여기에 라그랑주 역학을 사용한다고 하자, 너가 액션이 최소가 되는 경로로 선을 이었다고 치자, 근데 지금 니가 설정한 세계는 미분 기하학의 세게야 그러면 뭐다?
니가 방금 점 2개로 이은 액션이 최소가 되는 경로가 곧 측지선이라는 경로가 된다는 것 이해했겠지? 여전히 이해 안간다고? 그럼 그냥 넘어가고 이런 개념이 있다고 이해해
이게 아주 기초적인 미분기하학의 최소 에너지 원리야 이걸 이용하면, 자유 낙하, 1,2,3체 운동 모두 해석할 수 있는데 난 그냥 간단하게 자유낙하만 구현했으니 후에 관심있으면 찾아봐
import numpy as np
import matplotlib.pyplot as plt
s = np.linspace(0,40,1000)
h = s[1]-s[0]
m = 1
g = 9.8
def V(x,y):
return m*g*y
def RK4(f,X0,t):
n = len(t)
X = np.zeros((n,len(X0)))
X[0] = X0
for i in range(n-1):
k1 = f(X[i], t[i])
k2 = f(X[i]+0.5*h*np.array(k1),t[i]+0.5*h)
k3 = f(X[i]+0.5*h*np.array(k2),t[i]+0.5*h)
k4 = f(X[i]+h*np.array(k3),t[i]+h)
X[i+1] = X[i]+(h/6)*(np.array(k1)+2*np.array(k2)+2*np.array(k3)+np.array(k4))
return X
X0 = [0,5,1,0]
E = 49.5
def f(X,s):
return
[X[2],X[3],m*g*X[2]*X[3]/(E-V(X[0],X[1])),m*g*(-X[2]**2+X[3]**2)/(2*(E-V(X[0],X[1])))]
X = RK4(f,X0,s)[:,0]
Y = RK4(f,X0,s)[:,1]
plt.plot(X,Y)
plt.xlim((0,1))
plt.ylim((0,5))
plt.show()
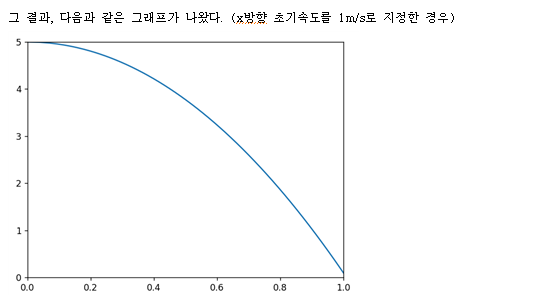
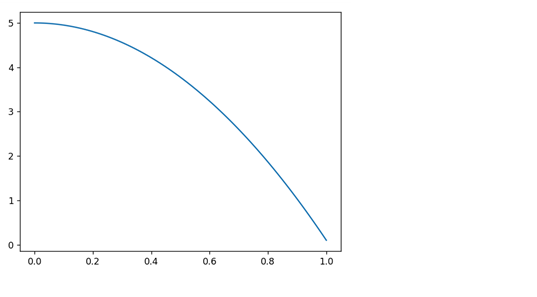
위에꺼가 뉴턴역학 그래프고, 아래꺼가 미분 기하학 그래프야
by. 1317 이종인
'로고스토리' 카테고리의 다른 글
| [로고스토리] 게이지 변환(Gauge Transformation) (0) | 2024.02.20 |
|---|---|
| [로고스토리] 장(Field)과 선속(Flux) (1) | 2024.01.28 |
| [로고스토리] RC필터와 3-way 스피커 (2) | 2024.01.03 |
| [로고스토리] 확산 문제를 위한 유한체적법 (2) | 2024.01.01 |
| [로고스토리] 표준모형과 입자검출방식의 이해 (1) | 2023.12.26 |



