[로고스토리] 확산 문제를 위한 유한체적법
유한체적법(Finite Volume Method, FVM)이란 편미분방정식을 검사체적에 대해 적분하여 방정식을 푸는 수치해석 방법입니다. 유한체적법에선 이러한 적분 과정이 다른 기법과 구분짓는 중요한 단계임을 기억해야 합니다. 가장 간단한 수송 과정(정상상태에서의 순수확산)에 대한 문제를 풀어보면 유한체적법에 대하여 이해하는데 도움이 될 것입니다. 또한 수치해석 결과를 엄밀해(analytic solution)와 비교함으로써 유한체적법의 정확성을 확인할 수 있을 것입니다.
유한체적법의 과정은 크게 3가지로 나눌 수 있습니다.
1단계: 격자 생성(Grid generation)
유한체적법의 첫 번째 단계는 해석영역을 이산화된 검사체적으로 나누는 과정입니다.
2단계: 이산화(Discretisation)
유한체적법의 두 번째 단계는 지배방정식을 검사체적에 대해 적분하여 이산화 방정식을 구합니다.
3단계: 방정식의 해(Solution of equations)
이산화 방정식을 경계조건을 반영하여 선형대수 방정식으로 수정한 후 적절한 행렬 해석기법을 이용하여 해를 구합니다.
정상상태 확산에 대한 지배방정식은 일반적인 수송방정식에서 시간변화 항과 대류 항을 무시함으로써 아래와 같이 나타낼 수 있습니다.

위 식을 검사체적에 대해서 적분하면 다음과 같습니다.

지금부터는 본격적으로 확산 문제를 풀어보며 유한체적법에 대해 알아보도록 하겠습니다.
앞서 소개한 정상상태 확산에 대한 지배방정식을 1차원에서 생각한다면 다음과 같습니다.

$\Gamma$는 확산계수, S는 소스 항

1. 격자 생성

다음과 같이 공간에 여러 개의 절점(nodal point)을 위치시키고, 절점의 중간에 검사체적의 경계를 위치시키면
검사체적의 폭 $\Delta x = \delta x_{wc}$ 임을 알 수 있습니다.
2. 이산화
지배방정식을 검사체적에 대해 적분하여 절점 P에서 이산화 방정식을 구합니다.

A는 검사체적의 단면적, $\Delta V$는 체적, $\overline{S}$는 소스 S를 검사체적에 대해 평균한 값
이 식은 결국 검사체적에 대한 $\phi$의 평형 방정식을 나타내며, 이산화 방정식의 유용한 형태를 유도하기 위해 확산계수$\Gamma $와 $\frac{d\phi }{dx}$가 필요합니다. $\Gamma$와 $\phi$는 절점에서 정의되기 때문에 검사체적 면에서 gradient를 계산하기 위해 절점 사이의 공간에서 물리량의 분포를 근사할 필요가 있으며, 중심차분법(central differencing)을 이용합니다. 소스 항 또한 $\overline{S}\Delta V = S_u + S_p\phi_P$로 선형적으로 근사하여 식을 정리하면 아래의 식이 됩니다.

3. 방정식의 해

1차원 정상상태 전도 열전달에 관한 문제를 통해 이 방정식의 해를 구하는 과정에 대해서 알아보겠습니다. 봉의 양 끝단이 온도 100와 500로 일정하게 유지되는 단열 봉에서 소스 항이 없다고 가정하면



절점 2, 3, 4에 대한 이산화 방정식
$a_PT_P=a_WT_W+a_ET_E$
경계 절점 1에 대한 이산화 방정식
$a_PT_P=a_WT_W+a_ET_E+S_u$
경계 절점 5에 대한 이산화 방정식
$a_PT_P=a_WT_W+a_ET_E+S_u$
이산화 과정을 통해 각 절점에 대한 이산화 방정식을 유도할 수 있고, 문제에서 주어진 값을 대입하면 이산화 방정식의 계수들도 모두 구할 수 있습니다. 아래의 표는 각각의 계수들을 정리한 표입니다.

따라서 이를 대수 방정식으로 표현하면

이 방정식들을 행렬 형태로 나타내면

이 문제의 엄밀해는 $T=800x+100$라고 합니다. 그렇다면 유한체적법을 이용한 수치해석 결과와 엄밀해를 비교해보면 다음과 같습니다.

2차원 확산 문제도 1차원과 동일한 방법으로 유도할 수 있습니다.
2차원 정상상태 확산의 지배방정식

1. 격자 생성

2. 이산화 방정식

3차원 확산 역시도 동일합니다.
3차원 정상상태 확산의 지배방정식

1. 격자 생성
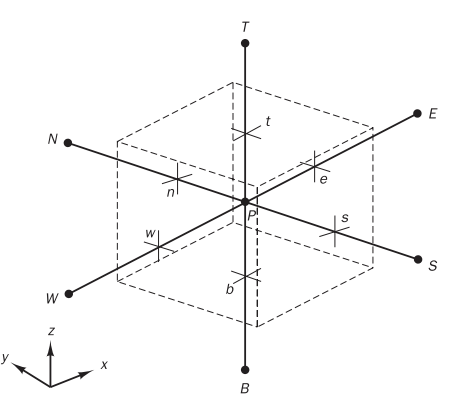
2. 이산화 방정식


by. 박종윤